Visit every node once?
2 approaches
- Breadth-first search(BFS)
- Depth-first search(DFS)
- Pre-order
- Post-order
- In-order
Breadth-first search(DFS) - horizontally
We want to visit every node on the same level, every sibling node before we look at a child. (horizontally)
Steps - Iteratively
- Create a queue (FIFO, this can be an array) and a variable to store the values of nodes visited
- Place the root node in the queue
- Loop as long as there is anything in the queue
- Dequeue a node from the queue and push the value of the node into the variable that stores the nodes
- If there is a left property on the node dequeued - add it to the queue
- If there is a right property on the node dequeued - add it to the queue
- return at the very end after the loop return the variable that stores all of our values.
Depth-first search(DFS) - vertically
Common: On every node we traverse the left, then we visit the node, then we traverse the right.
PreOrder
We're going to visit the node first. Then we look at the entire left side, we traverse the left, then we traverse the right, and that's true for any node
steps-recursively
- create a variable just like we did before, to store the values that we visited.
- Then we're going to create a variable called Current and just store the root of the tree in there.
- We're going to write a second helper function(traverse) which accepts a node
- we push the value of the node to the variable that stores our values that we return to the end.
- So we visit the node by adding it to the array or to the list.
- if the node has a left property
- call the helper function with the left property on the node
- if the node has a right property
- call the helper function with the right property on the node
Post-order
take a look at left and rightf first, then push
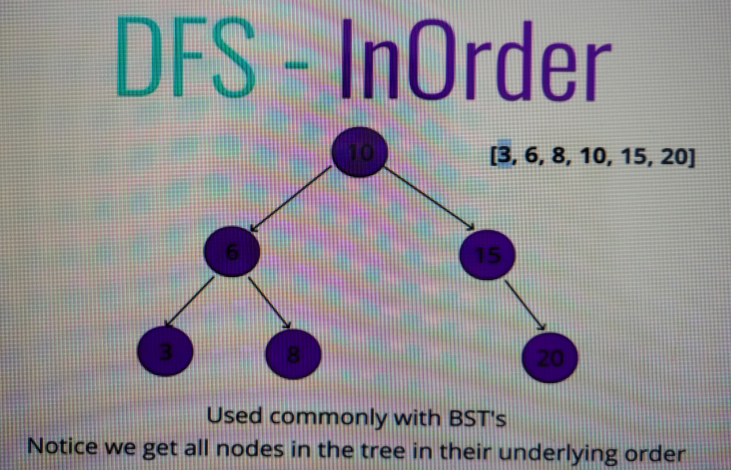
In Order
in order we're going to traverse the entire left side, then visit the node and then traverse the entire right side.
BFS? DFS?
time complexity is same, space complexity matters (depends on the structure)
BFS: More nodes to keep track of
DFS: Fewer nodes to keep track of
InOrder: array is in order, low to high, Used commonly with BST's.
PreOrder: Can be used to 'export' a tree structure so that is is easily reconstructed or copied - you know what the root it

'알고리즘' 카테고리의 다른 글
| Binary heap (0) | 2023.05.01 |
|---|---|
| [Binary search trees] Insert, find (0) | 2023.04.16 |
| [stacks & queues] queues (0) | 2023.04.09 |
| [stacks & queues] stack (0) | 2023.04.09 |
| insert, remove, reverse (0) | 2023.03.26 |