[Intermediate Sorting Algotithms] Quick sort

What is Quick sort

• Like merge sort, exploits the fact that arrays of 0 or 1 element are always sorted
• Works by selecting one element(called the 'pivot) and finding the index where the pivot should end up in sorted array
• Once the pivot is positioned appropriately, quick sort can be applied on either side of the pivot

 

How does it work?

https://visualgo.net/en/sorting

Sorting (Bubble, Selection, Insertion, Merge, Quick, Counting, Radix) - VisuAlgo

 

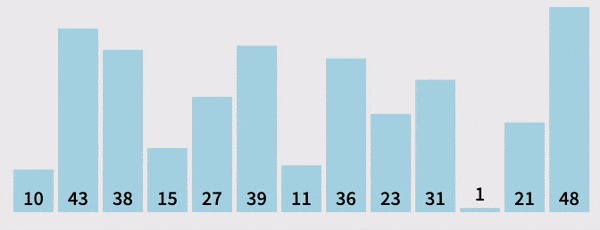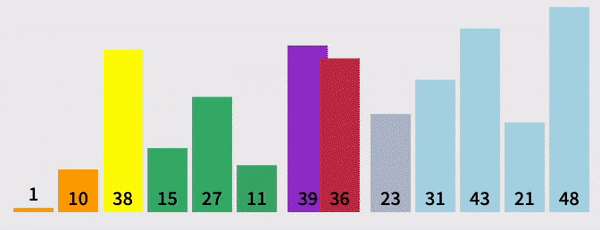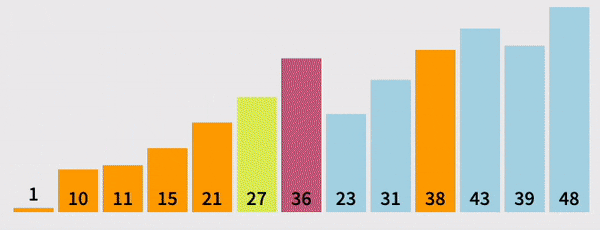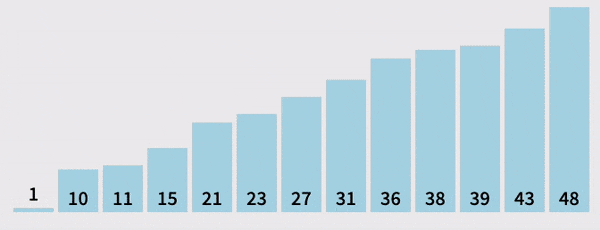
Pivot(partition) Helper

Just like the merge sort where we implemented merge helper, we do the same with quick sort.

한 pivot을 기준으로 왼쪽엔 더 작은 수, 오른쪽엔 더 큰 수로 나누게 해주는 역할

 

• In order to implement quick sort, it's useful to first implement a function resposible arranging elements in an array on either side of a pivot
• Given an array, this helper function should designate an element as the pivot
• It should then rearrange elements in the array so that all values less than the pivot are moved to the left of the pivot, and all values greater than the pivot are moved to the right of the pivot
• The order of elements on either side of the pivot doesn't matter
• The helper should do this in place, that is, it should not create a new array
• When complete, the helper should return the index of the pivot

Picking a pivot

• The runtime of quick sort depends in part on how one selects the pivot
• Ideally, the pivot should be chosen so that it's roughly the median value in the data set you're sorting
• For simplicity, we'll always choose the pivot to be the first element

 

Example

Pivot Pseudocode

• It will help to accept three arguments: 
  • an array, a start index, and an end index (these can default to 0 and the array length minus 1, respectively)
• Grab the pivot from the start of the array
• Store the current pivot index in a variable (this will keep track of where the pivot should end up)
• Loop through the array from the start until the end
  • If the pivot is greater than the current element, increment the pivot index variable and then swap the current element with the element at the pivot index
• Return the pivot "index"

function pivot(arr, start=0, end=arr.length+1) {
  function swap(array, i, j){
    var temp=array[i];
    array[i]=array[j];
    array[j]=temp;
  }

  var pivot = arr[start]
  var swapIdx=start;
  
  for(var i=start+1; i<arr.length;i++){
    if(pivot > arr[i]){
      swapIdx++;
      swap(arr, swapIdx,i)
      // console.log(arr)
    }
  }
swap(arr, start, swapIdx)
return swapIdx;//3
}

pivot([4,7,2,1,5,7,6,3])

//ES6
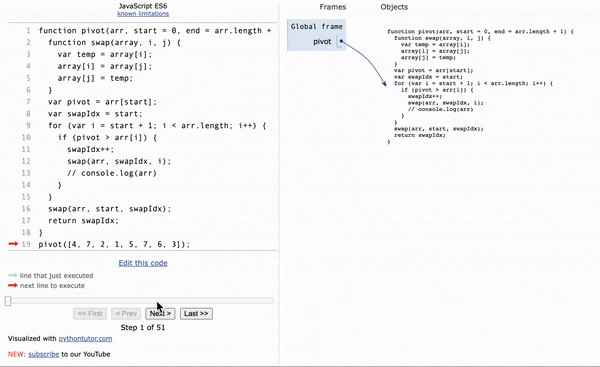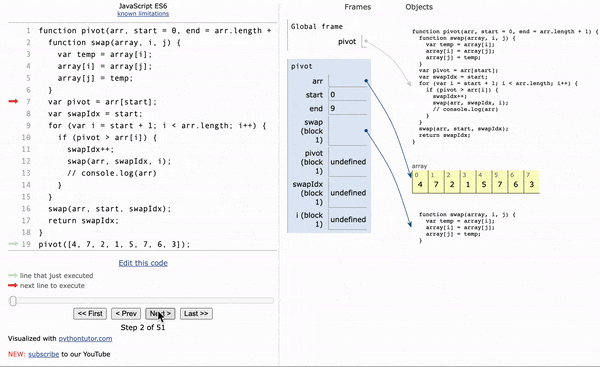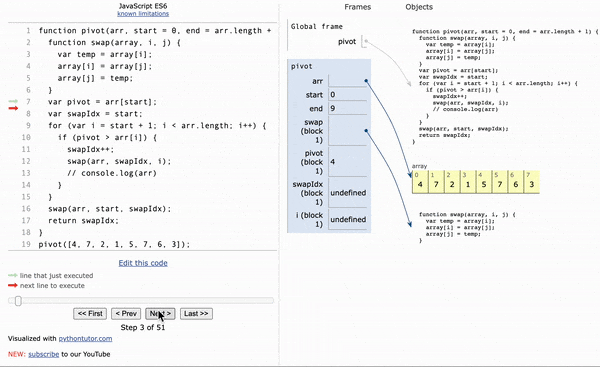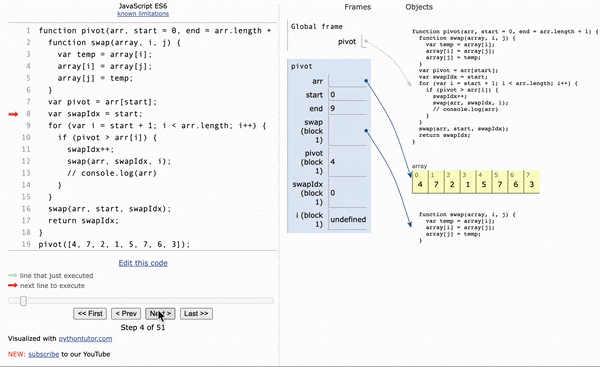
function pivot(arr, start=0, end=arr.length-1) {
  const swap=(arr,idx1,idx2) => {
    [arr[idx1], arr[idx2] = [arr[idx2], arr[idx1]]]
  }

  //we are assuming the pivot is always the first element
  let pivot =arr[start];
  let swapIdx=start;

  for(let i=start+1; i<= end; i++){
    if(pivot> arr[i]){
      swapIdx++;
      swap(arr,swapIdx,i)
    }
  }

  //swap the pivot from the start the swapPoint
  swap(arr,start,swapIdx);
  return swapIdx;
}

Quicksort Pseudocode

• Call the pivot helper on the array
• When the helper returns to you updated pivot index, recursively call the pivot helper on the subarray to the left of that index, and the subarray to the right of that index
• Your base case occurs when you consider a subarray with less than 2 elements

 

//pivot
function pivot(arr, start=0, end=arr.length-1) {
  const swap=(arr,idx1,idx2) => {
    [arr[idx1], arr[idx2] = [arr[idx2], arr[idx1]]]
  }
  //we are assuming the pivot is always the first element
  let pivot =arr[start];
  let swapIdx=start;

  for(let i=start+1; i<= end; i++){
    if(pivot> arr[i]){
      swapIdx++;
      swap(arr,swapIdx,i)
    }
  }
  //swap the pivot from the start the swapPoint
  swap(arr,start,swapIdx);
  return swapIdx;
}

//quick sort
function quickSort(arr, left = 0, right = arr.length - 1) {
  //base case
  if (left < right) {
    let pivotIndex = pivot(arr, left, right); //3
    //left
    quickSort(arr, left, pivotIndex - 1);
    //right
    quickSort(arr, pivotIndex + 1, right);
  }
  return arr;
}

quickSort([4, 6, 9, 1, 2, 5, 3]);

 

Big O of Quicksort

• Best: n log(n)
• Average: n log(n)
• Worst: O(n^2)